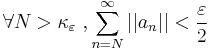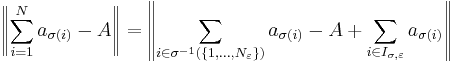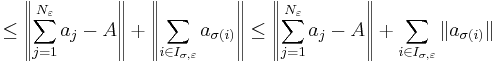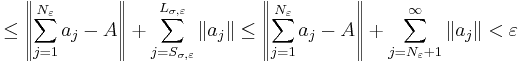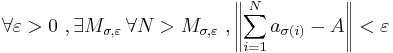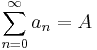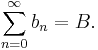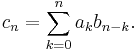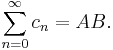Absolute convergence
In mathematics, a series (or sometimes also an integral) of numbers is said to converge absolutely if the sum (or integral) of the absolute value of the summand or integrand is finite. More precisely, a real or complex series 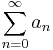 is said to converge absolutely if
is said to converge absolutely if 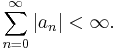
Absolute convergence is important to the study of infinite series because its definition is strong enough to have properties of finite sums that not all convergent series possess, yet is broad enough to occur commonly.
Contents |
Background
One may study the convergence of series 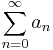 whose terms
whose terms 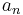 are elements of an arbitrary abelian topological group. The notion of absolute convergence requires more structure, namely a norm:
are elements of an arbitrary abelian topological group. The notion of absolute convergence requires more structure, namely a norm:
A norm on an abelian group G (written additively, with identity element 0) is a real-valued function 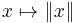 on G such that:
on G such that:
- The norm of the identity element of G is zero:
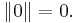
- For every x in G,

- For every x in G,
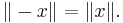
- For every x, y in G,

Then the function 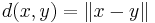 induces on G the structure of a metric space (in particular, a topology). We can therefore consider G-valued series and define such a series to be absolutely convergent if
induces on G the structure of a metric space (in particular, a topology). We can therefore consider G-valued series and define such a series to be absolutely convergent if 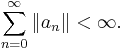
Relation to convergence
If the metric d on G is complete, then every absolutely convergent series is convergent. The proof is the same as for complex-valued series: use the completeness to derive the Cauchy criterion for convergence—a series is convergent if and only if its tails can be made arbitrarily small in norm—and apply the triangle inequality.
In particular, for series with values in any Banach space, absolute convergence implies convergence. The converse is also true: if absolute convergence implies convergence in a normed space, then the space is a Banach space.
If a series is convergent but not absolutely convergent, it is called conditionally convergent. An example of a conditionally convergent series is the alternating harmonic series. Many standard tests for divergence and convergence, most notably including the ratio test and the root test, demonstrate absolute convergence. This is because a power series is absolutely convergent on the interior of its disk of convergence.
Proof that any absolutely convergent series is convergent
Assume 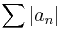 is convergent. Since a series of complex numbers converges if and only if both its real and imaginary parts converge, we may assume with equal generality that
is convergent. Since a series of complex numbers converges if and only if both its real and imaginary parts converge, we may assume with equal generality that 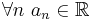 . Then,
. Then, 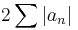 is convergent.
is convergent.
Since 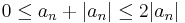 , we have:
, we have:
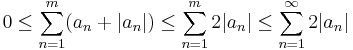 .
.
Thus, 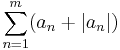 is a bounded monotonic sequence (in m), which must converge.
is a bounded monotonic sequence (in m), which must converge.
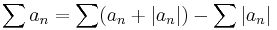 is a difference of convergent series; therefore, it is also convergent.
is a difference of convergent series; therefore, it is also convergent. 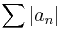 is convergent
is convergent 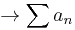 is convergent.
is convergent.
Rearrangements and unconditional convergence
In the general context of a G-valued series, a distinction is made between absolute and unconditional convergence, and the assertion that a real or complex series which is not absolutely convergent is necessarily conditionally convergent (meaning not unconditionally convergent) is then a theorem, not a definition. This is discussed in more detail below.
Given a series 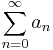 with values in a normed abelian group G and a permutation
with values in a normed abelian group G and a permutation  of the natural numbers, one builds a new series
of the natural numbers, one builds a new series 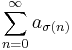 , said to be a rearrangement of the original series. A series is said to be unconditionally convergent if all rearrangements of the series are convergent to the same value.
, said to be a rearrangement of the original series. A series is said to be unconditionally convergent if all rearrangements of the series are convergent to the same value.
When G is complete, absolute convergence implies unconditional convergence.
Theorem
Let 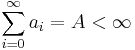 ,
, 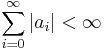 and let
and let  be a permutation of
be a permutation of 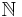 , then
, then 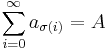
Proof
For any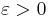 , we can choose some
, we can choose some 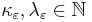 , such that
, such that
and
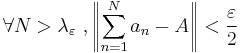 .
.
let 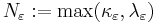 ,
, 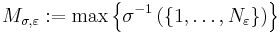 .
.
For any 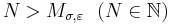 , let
, let
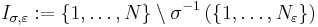 ,
,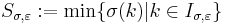 (note.
(note.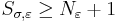 ), and
), and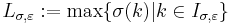
then
therefore
then 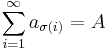
The issue of the converse is much more interesting. For real series it follows from the Riemann rearrangement theorem that unconditional convergence implies absolute convergence. Since a series with values in a finite-dimensional normed space is absolutely convergent if each of its one-dimensional projections is absolutely convergent, it follows easily that absolute and unconditional convergence coincide for 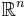 -valued series.
-valued series.
But there is an unconditionally and nonabsolutely convergent series with values in Hilbert space 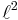 : if
: if 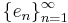 is an orthonormal basis, take
is an orthonormal basis, take 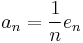 .
.
A theorem of Dvoretzky-Rogers asserts that every infinite-dimensional Banach space admits an unconditionally but non-absolutely convergent series.
Products of series
The Cauchy product of two series converges to the product of the sums if at least one of the series converges absolutely. That is, suppose:
The Cauchy product is defined as the sum of terms 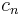 where:
where:
Then, if either the 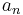 or
or 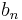 sum converges absolutely, then
sum converges absolutely, then
Absolute convergence of integrals
The integral 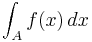 of a real or complex-valued function is said to converge absolutely if
of a real or complex-valued function is said to converge absolutely if 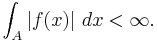 One also says that
One also says that  is absolutely integrable.
is absolutely integrable.
When ![A = [a,b]](/2012-wikipedia_en_all_nopic_01_2012/I/ba837ba984a838727bc61252ee67457f.png) is a closed bounded interval, every continuous function is integrable, and since
is a closed bounded interval, every continuous function is integrable, and since  continuous implies
continuous implies 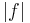 continuous, similarly every continuous function is absolutely integrable. It is not generally true that absolutely integrable functions on
continuous, similarly every continuous function is absolutely integrable. It is not generally true that absolutely integrable functions on ![[a,b]](/2012-wikipedia_en_all_nopic_01_2012/I/2c3d331bc98b44e71cb2aae9edadca7e.png) are integrable: let
are integrable: let ![S \subset [a,b]](/2012-wikipedia_en_all_nopic_01_2012/I/1c4412382a7e6967fa515506b9ec2bbc.png) be a nonmeasurable subset and take
be a nonmeasurable subset and take 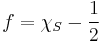 , where
, where 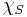 is the characteristic function of S. Then
is the characteristic function of S. Then  is not Lebesgue measurable but
is not Lebesgue measurable but 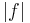 is constant. However, it is a standard result that if
is constant. However, it is a standard result that if  is Riemann integrable, so is
is Riemann integrable, so is 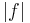 . This holds also for the Lebesgue integral; see below. On the other hand a function
. This holds also for the Lebesgue integral; see below. On the other hand a function  may be Kurzweil-Henstock integrable (or "gauge integrable") while
may be Kurzweil-Henstock integrable (or "gauge integrable") while 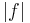 is not. This includes the case of improperly Riemann integrable functions.
is not. This includes the case of improperly Riemann integrable functions.
Similarly, when  is an interval of infinite length it is well-known that there are improperly Riemann integrable functions
is an interval of infinite length it is well-known that there are improperly Riemann integrable functions  which are not absolutely integrable. Indeed, given any series
which are not absolutely integrable. Indeed, given any series 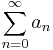 one can consider the associated step function
one can consider the associated step function 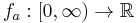 defined by
defined by 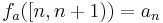 . Then
. Then 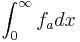 converges absolutely, converges conditionally or diverges according to the corresponding behavior of
converges absolutely, converges conditionally or diverges according to the corresponding behavior of 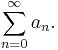
Another example of a convergent but not absolutely convergent improper Riemann integral is 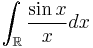 .
.
On any measure space A the Lebesgue integral of a real-valued function is defined in terms of its positive and negative parts, so the facts:
 integrable implies
integrable implies 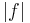 integrable
integrable measurable,
measurable, 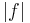 integrable implies
integrable implies  integrable
integrable
are essentially built into the definition of the Lebesgue integral. In particular, applying the theory to the counting measure on a set  , one recovers the notion of unordered summation of series developed by Moore-Smith using (what are now called) nets. When
, one recovers the notion of unordered summation of series developed by Moore-Smith using (what are now called) nets. When 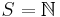 is the set of natural numbers, Lebesgue integrability, unordered summability and absolute convergence all coincide.
is the set of natural numbers, Lebesgue integrability, unordered summability and absolute convergence all coincide.
Finally, all of the above holds for integrals with values in a Banach space. The definition of a Banach-valued Riemann integral is an evident modification of the usual one. For the Lebesgue integral one needs to circumvent the decomposition into positive and negative parts with Daniell's more functional analytic approach, obtaining the Bochner integral.
See also
- Convergence of Fourier series
- Conditional convergence
- Modes of convergence (annotated index)
- Cauchy principal value
- A counterexample related to Fubini's theorem
- 1/2 − 1/4 + 1/8 − 1/16 + · · ·
- 1/2 + 1/4 + 1/8 + 1/16 + · · ·
References
- Walter Rudin, Principles of Mathematical Analysis (McGraw-Hill: New York, 1964).